Le raccordement curviligne de moulures : méthode analytique et compléments

- Démonstration analytique
Partons de la Fig. 1 pour conduire le raisonnement analytique.
Notons O1 et O2 les centres des deux arcs de moulure circulaire et plaçons le point O au milieu du segment O1 O2. O est pris comme origine d'un repère orthogonal OxOy, Ox passant par O1 et O2.
Supposons que l’abscisse du point O2 vaille c, donc par construction -c pour l’abscisse du point O1. Posons également r2 - r1 = 2a. Prenons un point M, avec comme coordonnées x et y. Exprimons que la différence des rayons au point M est égale à 2a :
MO2 - MO1 = 2a, soit MO2 = MO1 + 2a
Élevons au carré :
(MO2)2 = (MO1)2 + 4aMO1 + 4a2
Soit en valeurs algébriques :
(x - c)2 + y2 = (x+c)2 + y2 + 4aMO1 + 4a2
Développons :
x2 - 2cx + c2 + y2 = x2 + 2cx + c2 + y2 + 4aMO1 + 4a2
Simplifions :
4cx + 4a2 = - 4aMO1
cx + a2 = - aMO1
Élevons de nouveau au carré chaque membre :
c2x2 + 2a2cx + a4 = a2(MO1)2
c2x2 + 2a2cx + a4 = a2((x + c)2 + y2)
c2x2 + 2a2cx +a4 = a2x2 + 2a2cx + a2c2 + a2y2
Soit :
x2(c2-a2) – a2y2 = a2c2 – a4
Posons b2 = c2 – a2
x2b2 -a2y2 =a2b2
Divisons les deux membres par a2b2 :
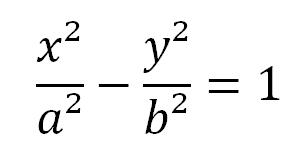
On retrouve ainsi l'équation d'une hyperbole.
- Tracer numériquement ce raccord
Dans son tableur, la première colonne comporte les valeurs des abscisses x.
La seconde colonne contient la formule b²(x²/a² - 1).
La troisième colonne donne les valeurs de y, en prenant la racine carrée de la seconde colonne.
Faisons varier x de -5 à -20, avec un pas de 0,5 cm.
Nous obtenons en colonne 3 les valeurs de y correspondantes.
Il suffit alors de sélectionner les colonnes 1 et 3 et de demander l'insertion d'un graphique xy, en spécifiant que le style est un tracé continu. Ce tracé apparait dans un graphique à part. Il suffit alors d'imprimer ce tracé à l'échelle 1 puis de le recopier au dos de chacune des deux moulures ou sur un gabarit qui servira pour l'usinage.
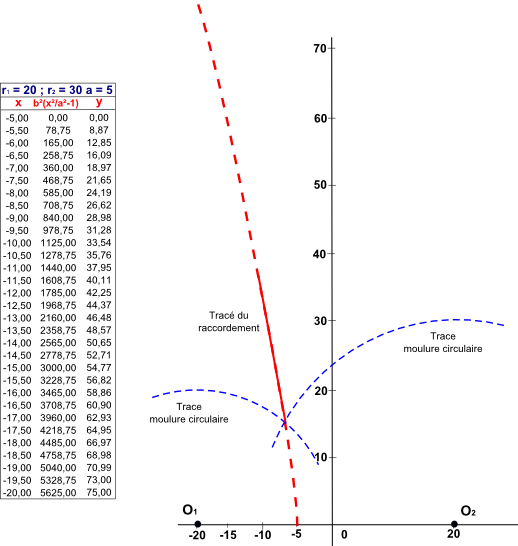
À titre d'exemple, la Fig. 2 est l'image du tableur, donnant pour un rayon r1 de 20 cm, un rayon r2 de 30 cm et une distance entre centres de 40 cm les coordonnées des points de l'hyperbole pour une variation de x centimètre par centimètre.
- Remarque sur la troisième méthode, approximation par un arc de cercle
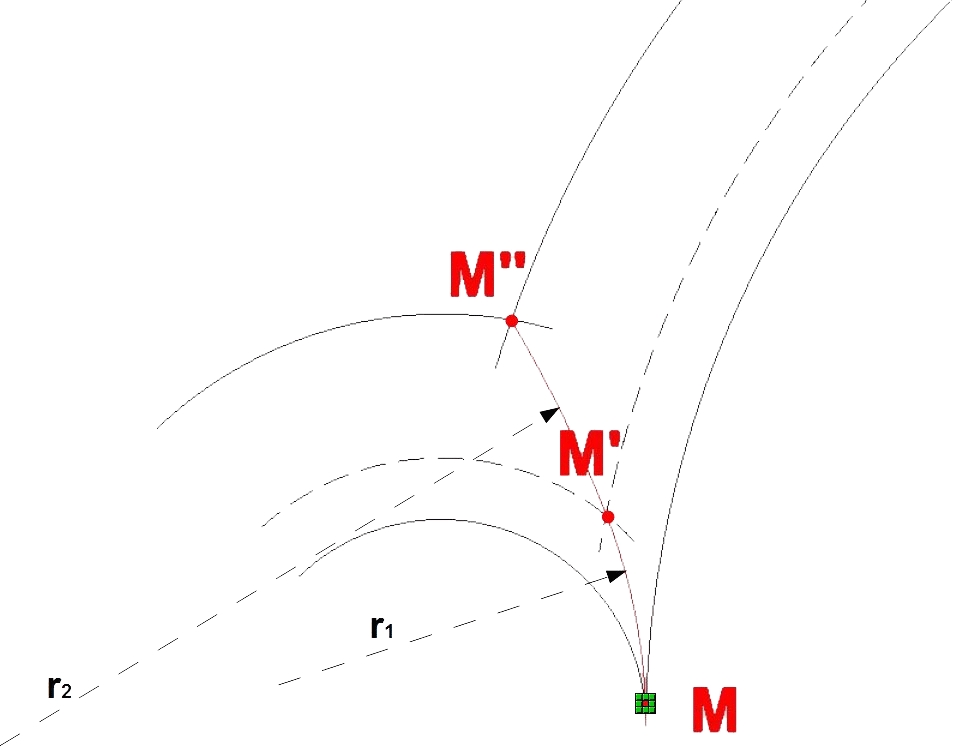
Un lecteur m'a fait remarquer que, dans le cas où la différence des rayons des moulures était importante et que la pointe du raccord se trouvait près du sommet de l'hyperbole (donc sur la ligne qui joint les centres des arcs de moulures), il y avait lieu d'utiliser non pas un arc de cercle pour tracer le raccord, mais deux, voire trois arcs de cercles tangents, de rayons différents. Sur la Fig. 3, où l'on utilise deux arcs, un premier, de faible rayon, joint les points M et M' ; un second arc, de rayon plus important, joint M' à M'', les deux arcs étant naturellement tangents au point M' . Cette méthode, avec deux ou trois arcs, est du reste proposée dans le monumental Traité d'ébénisterie de Lucien Chanson.
Sans vouloir en rien m'inscrire en faux contre cette idée, je recommande simplement, plutôt que de tracer deux, voire trois, arcs de cercles tangents, de tracer par points l'arc d'hyperbole : c'est à la fois plus simple (voir la quatrième méthode), plus rapide et plus précis.
Cela étant, en atelier, rien n'empêche de tracer deux ou trois arcs tangents : le résultat sera aussi satisfaisant.
- Cas de moulures non coplanaires et de rayons différents
Page 26 de l’article du Bouvet 159, sous le titre « Cas des moulures non coplanaires », nous avons écrit « avoir traité le cas de moulures à dos coplanaires ». Comme tous les exemples donnés jusqu'alors ont été pris dans un plan horizontal, nous aurions dû écrire « à bases coplanaires » et ne pas parler ici de dos.
Le cas de moulures non coplanaires et de rayons différents a été illustré dans l'article avec la Fig. 26 page 29. Il a bien été précisé qu'un tel raccord n'était acceptable qu'avec les trois conditions suivantes :
- la différence des rayons des deux moulures n'est pas trop importante,
- l'épaisseur des moulures n'est pas trop forte
- l'angle du dièdre n'est pas trop fermé.
Sans ces trois conditions, le raccordement présentera des désaffleurs d'autant plus importants que l'une de ces conditions ne sera pas satisfaite, et bien sûr encore plus si ces trois conditions ensemble ne sont pas réunies.
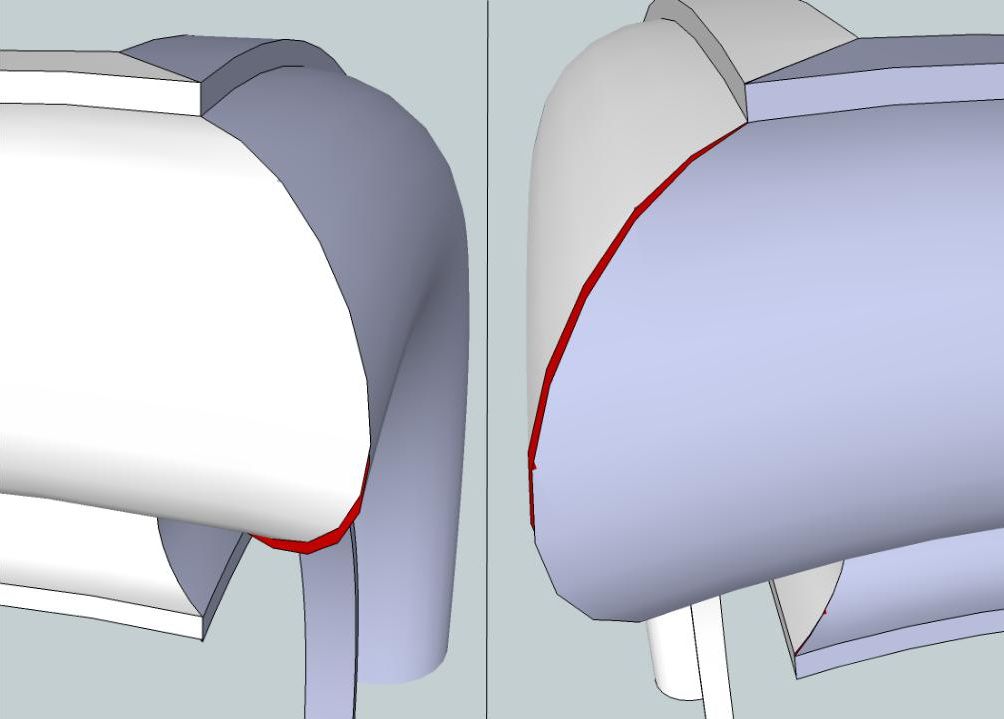
Pour nous en convaincre, la Fig. 4 donne l'exemple d'un raccordement de moulures de 10 cm de large et de 5 cm d'épaisseur, l'une des moulures ayant un rayon interne de 20 cm et l'autre de 50 cm. On remarque clairement les désaffleurs marqués en rouge ; à certains endroits, l'écart est de près de 2 mm. Aucun espoir de pouvoir reprendre un tel raccord un tant soit peu proprement.
Nous avons indiqué que l'on pouvait « tricher » un peu. Voyons comment procéder, sans néanmoins craindre une quelconque réprimande !
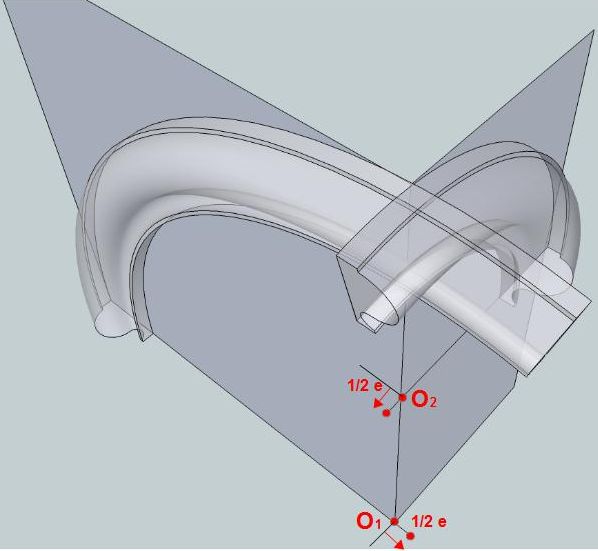
On avance chacune des moulures d'une demi épaisseur (soit ½ e), leur centre se trouvant ainsi en avant de l'arête du dièdre comme le montre la Fig. 5. Il y aura lieu également de relever très légèrement l'une des moulures.
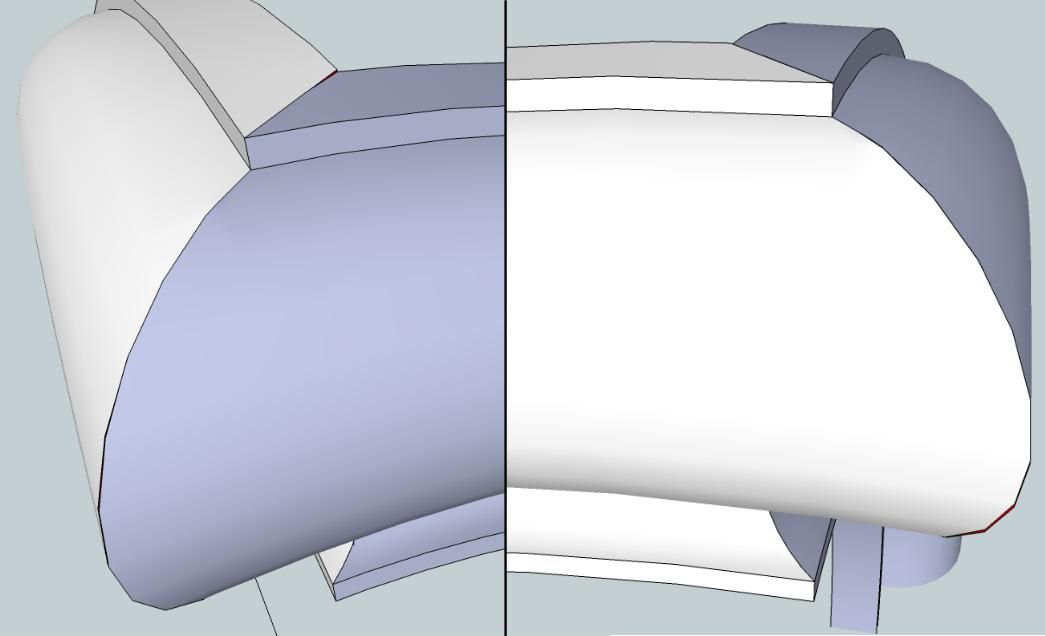
Regardons le résultat sur la Fig. 6. La configuration est bien différente et ne nécessitera qu'un ponçage un peu soigné pour bien atténuer les désaffleurs, plus nombreux certes, mais de moindre importance, étant de moins de 5 dixièmes de mm pour les plus importants. Pourtant il s'agit bien des deux mêmes moulures.
On voit un désaffleur qui est apparu sur la partie haute et plate du raccordement. Il y en a aussi sur les parties basses. Par contre, ceux-ci sont de l'ordre de 1 à 2 dixièmes de millimètre, donc assez aisés à reprendre. Rien de magique dans ce résultat : il provient juste d'une analyse de la configuration géométrique et de la déduction des bonnes options à prendre.
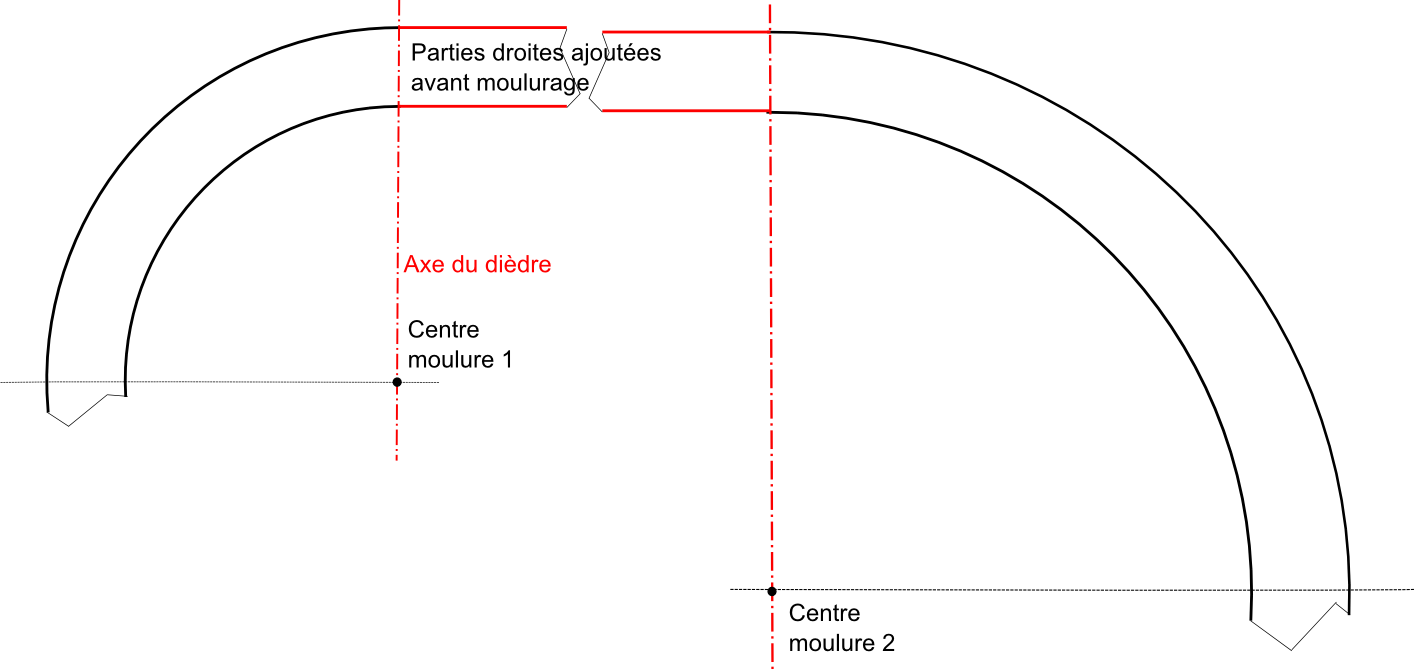
Cela étant, il existe une possibilité pour obtenir un raccord parfait. La Fig. 7 indique comment procéder, en prolongeant, au traçage de chaque pièce, l'arc de moulure par un petit segment de droite dans la partie du raccord. Cet artifice permet de revenir au raccordement de deux moulures droites. Cette solution suppose néanmoins de tracer et fabriquer les moulures circulaires avec ce segment droit, et seulement effectuer le moulurage ensuite.
Raccord de moulures curvilignes N° 159.
Bonjour.
L'astuce présentée n'est valable que si les deux moulures curvilignes, de rayons de courbures différents et respectant les conditons de tangence, sont posées sur un support dièdre SAILLANT.
Dans le cas d'un support dièdre RENTRANT, l'astuce n'est plus valable. Seul un reprofilage de l'une sera nécessaire pour un
raccord parfait. Les défauts apparents seront d'autant plus importants, si la différences des rayons de courbures est importante er si l'angle dièdre rentrant est plus fermé.
Les angles coupes d'onglets sont égaux. C'est la nature géométrique du joint plan d'assemblage qui impose le reprofilage. D'où le théorème suivant :
«Pour raccorder 2 moulures à géométrie plane quelconque, mais de profils identiques, coplanaires ou non coplanaires, il faut qu'il y est une symétrie parfaite par rapport au plan du joint d'assemblage.»
Dans le cas contraire, reprofilage assuré pour l'une des deux
moulures.
Pour apporter un plus.
Cordialement.
- Connectez-vous ou inscrivez-vous pour publier un commentaire

























Vos commentaires