Le raccordement mixtiligne de moulures : méthode analytique

• La méthode analytique

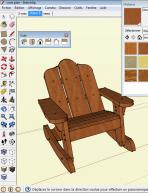
Prenons la Fig. 1 comme support (Fig. 15 dans l’article du Bouvet).

Le point M’ appartient à la fois au cercle externe de la moulure circulaire et au côté externe de la moulure droite. L’équation du cercle externe, centré en O, s’écrit :

x² + y² = (r + e)²

L’équation de la droite support du côté externe de la moulure droite est la suivante :

y = d + e

Les coordonnées du point M’ sont ainsi définies par le système d’équations :

(1) : x² + y² = (r + e)²

(2) : y = d + e

Si e varie, les équations (1) et (2) donnent le lieu géométrique des points situés sur le raccord de moulure.

De (2), on tire : e = y - d

En reportant dans (1), on obtient :

x² + y² = (r + (y-d))²

soit :

x² + y² = ((r – d) + y)²

Développons le second membre :

x² + y² = (r – d)² + 2y(r - d) + y²

Soit, en simplifiant et en changeant certains termes de côté :

2y(r-d) = x² – (r – d)²

Enfin, pour r étant différent de d, c’est-à-dire pour une moulure droite sécante et non tangente :

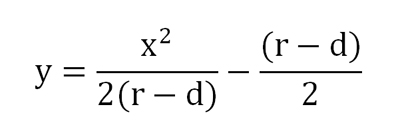
Les points appartenant au raccord de moulure sont sur la courbe donnée par cette équation.

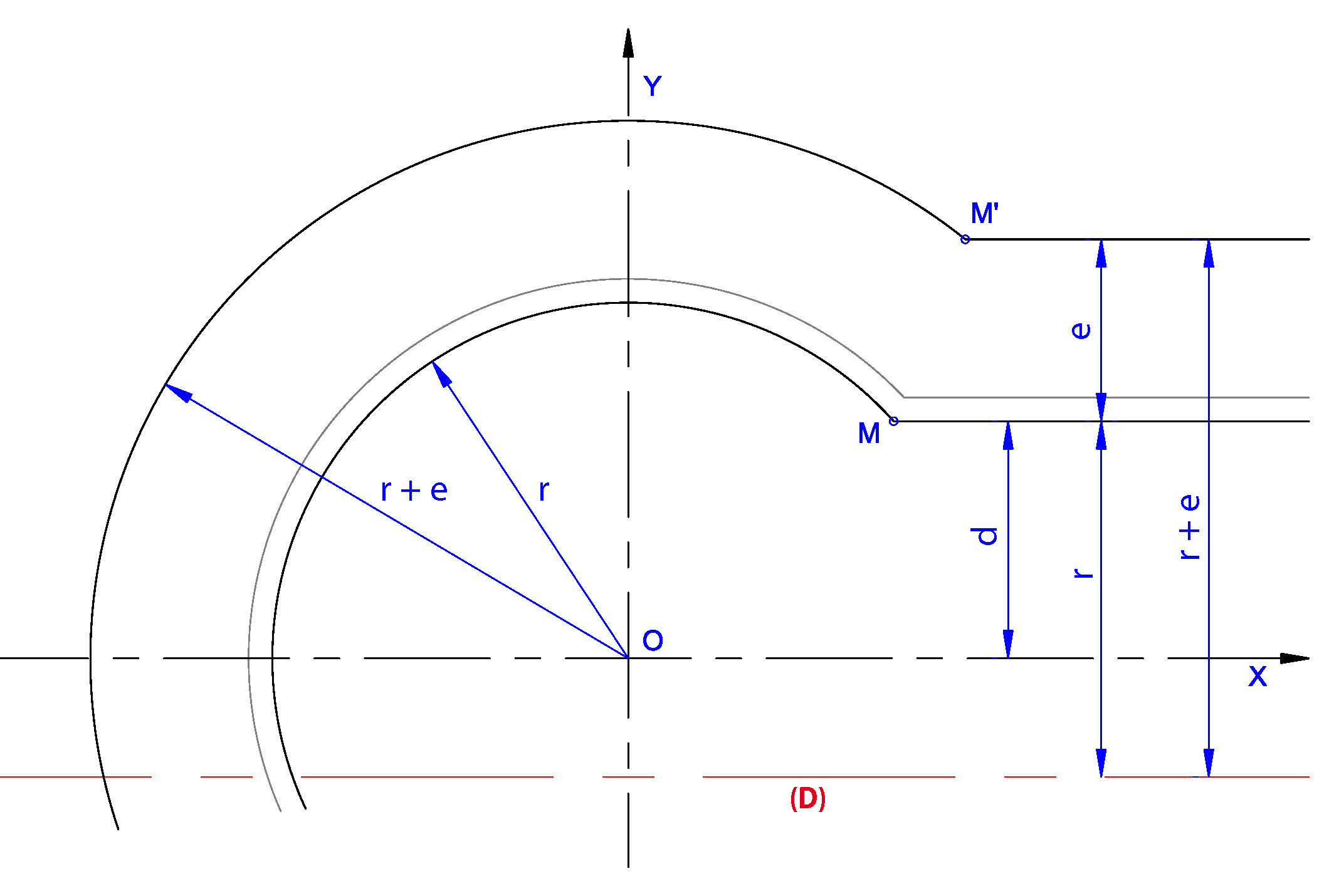
C’est bien sûr l’équation d’une parabole, un peu particulière néanmoins puisqu’elle ne comporte pas de terme en x, ceci provenant de la façon simplifiée dont le problème a été posé.

On retrouve aussi que l’ordonnée à l’origine, pour x = 0, est égale à (d – r) / 2, milieu sur l’axe Oy entre le foyer et la directrice (Fig. 2).

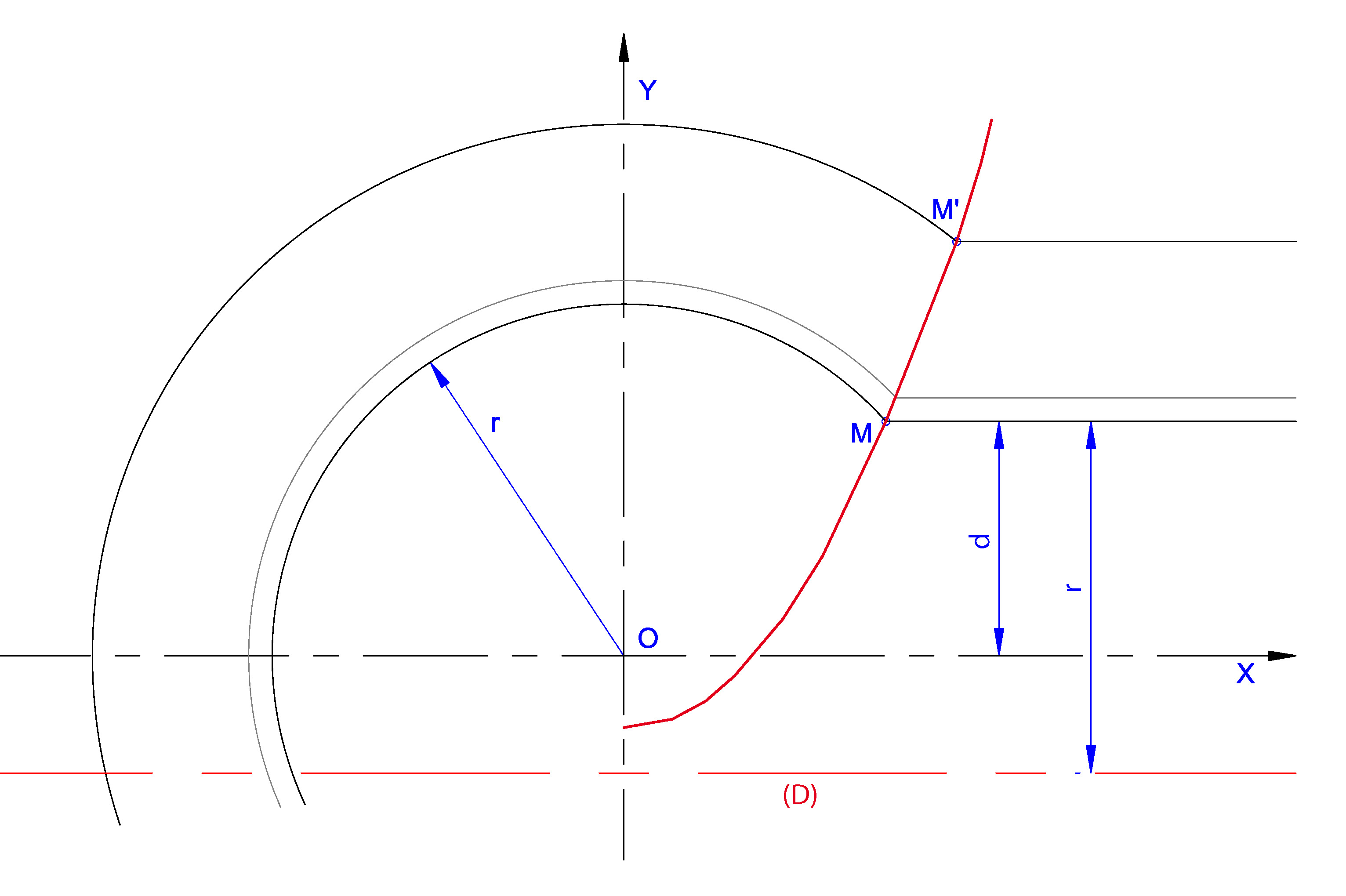
La Fig. 3 donne deux autres cas de raccords entre une moulure droite et une moulure circulaire (on se référera à l’article pour retrouver les cas 1 et 2).

Dans cette configuration, l’équation de cette parabole n’est plus la même que précédemment. L’équation du cercle externe de la moulure circulaire, centré en O, reste identique, en s’écrivant:

x² + y² = (r + e)²

Par contre, l’équation de la droite support du côté externe de la moulure droite change, en devenant la suivante :

y = d - e

Les coordonnées du point M’ sont ainsi définies par le système d’équations :

(1) : x² + y² = (r + e)²

(2) : y = d - e

Si e varie, les équations (1) et (2) donnent le lieu géométrique des points situés sur le raccord de moulure.

De (2), on tire : e = d - y

En reportant dans (1), on obtient :

x² + y² = (r + (d - y))²

soit :

x² + y² = ((r + d) - y)²

Développons le second membre :

x² + y² = (r + d)² - 2y(r + d) + y²

Soit en simplifiant et en changeant de côté certains termes :

2y(r + d) = - x² + (r + d)²

Enfin, pour r étant différent de - d, c’est à dire pour une moulure droite sécante et non tangente :

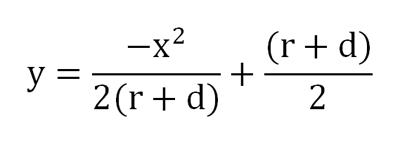
La parabole, avec un coefficient négatif pour le terme en x², est cette fois ouverte côté des ordonnées négatives.

• Comment tracer ce raccord ?

Nous avons indiqué cinq méthodes pour tracer ce raccord. Pour qui possède un tableur avec grapheur sur son ordinateur, il existe une sixième méthode.

Comme nous connaissons l’équation de la parabole, il est facile de calculer chacun de ses points et d’en tracer la courbe.

Dans son tableur, la première colonne comporte les valeurs des abscisses x, variant de 0 à 30.

La seconde colonne contient la formule 1/2x²(r - d).

La troisième colonne donne les valeurs de y, avec la formule « seconde colonne » -(r - d) / 2.

Il suffit alors d’insérer le résultat graphique des première et troisième colonnes (x et y) en spécifiant que l’on désire une courbe continue. Le tracé apparait dans un graphique à part.

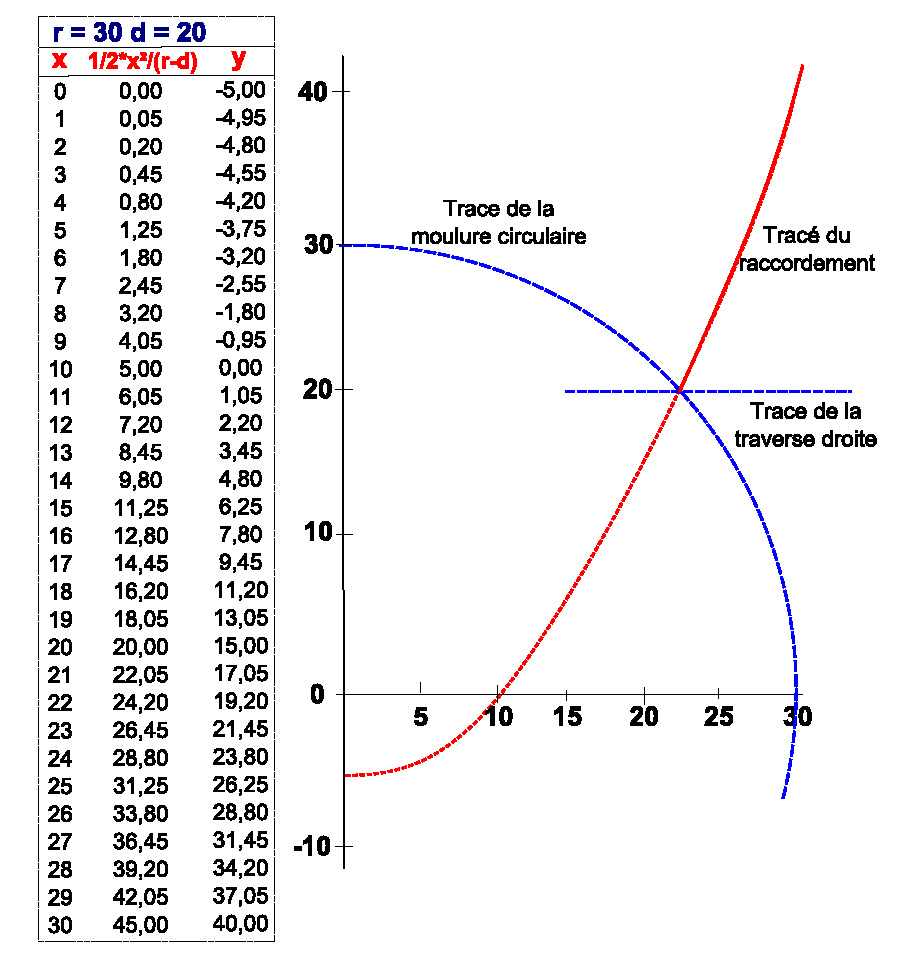
À titre d’exemple, la Fig. 4 est l’image du tableur, donnant pour un rayon r de 30 cm et une distance d de 20 cm les coordonnées des points de la parabole, pour une variation de x centimètre par centimètre. On imprimera à l’échelle ce tracé, que l’on reportera sur le dos de chaque moulure ou sur des gabarits, avant d’effectuer les découpes.